Introduction:
Diffractive Optical Elements (DOEs) are optical components that use the wave characteristics of light to manipulate it. This is achieved using thin micro-structure patterns that alter the phase of light passing through the DOE. By designing these microstructures properly, the light can be manipulated to achieve almost any desired intensity profile or shape. This technology offers many functions and light manipulations that are not possible with standard Conventional optics such as Refractive and Reflective optics. These functions are extremely useful in many applications and can significantly improve system performance. In this article, we will discuss how DOEs can address the problems associated with conventional optics in automotive lighting and how they can be designed to achieve different intensity patterns for signalling purposes.
Problem of Conventional optics in the automobile
The problems associated with conventional optics in automobile taillights and headlights are like those in other applications, including limited visibility, energy inefficiency, and glare. However, there are also some specific challenges associated with these lighting systems. One of the primary problems with conventional taillights is that they often rely on incandescent/ halogen bulbs, which can be relatively energy inefficient and have a shorter lifespan than other types of bulbs. This can lead to higher maintenance costs and increased environmental impact. In addition, conventional taillights may not provide sufficient brightness or visibility in low-light or poor weather conditions.
Similarly, conventional lights may also have limited visibility and can cause glare that can reduce the visibility of other drivers on the road. This can be particularly problematic when driving in adverse weather conditions or on poorly lit roads.
Diffractive optics can offer some advantages over conventional optics in both taillights and headlights. By using microscopic surface patterns, diffractive optics can manipulate light to improve visibility and reduce glare while also increasing energy efficiency. Additionally, diffractive optics can be used to create customized lighting patterns and shapes, which can help enhance the aesthetic appeal of automobiles. More research and development are needed to ensure that diffractive optics can be effectively integrated into automobile taillights and headlights. Major advantages of Diffractive Optics over conventional optics are like:
The Diffraction Phenomenon:
Diffraction occurs when a wave’s lateral extent is restricted. In the case of DOEs, diffraction is achieved using micro-structured patterns to manipulate light waves. DOEs use thin micro-structures to diffract light waves, producing specific patterns of light that can be used in a variety of applications. For example, DOEs are used in automobile lamps to control the direction and intensity of light emissions, reducing glare and improving visibility for drivers. The ability to precisely control the shape and intensity of light using DOEs provides a powerful tool for manipulating light in a variety of ways, opening new possibilities in optics and photonics. Overall, diffraction phenomena using DOEs provide a versatile and powerful tool for manipulating light waves, with applications in a wide range of fields including automotive lighting, holography, and optical communication.
The Diffraction Phenomenon:
Diffraction occurs when a wave’s lateral extent is restricted. In the case of DOEs, diffraction is achieved using micro-structured patterns to manipulate light waves. DOEs use thin micro-structures to diffract light waves, producing specific patterns of light that can be used in a variety of applications. For example, DOEs are used in automobile lamps to control the direction and intensity of light emissions, reducing glare and improving visibility for drivers. The ability to precisely control the shape and intensity of light using DOEs provides a powerful tool for manipulating light in a variety of ways, opening new possibilities in optics and photonics. Overall, diffraction phenomena using DOEs provide a versatile and powerful tool for manipulating light waves, with applications in a wide range of fields including automotive lighting, holography, and optical communication.
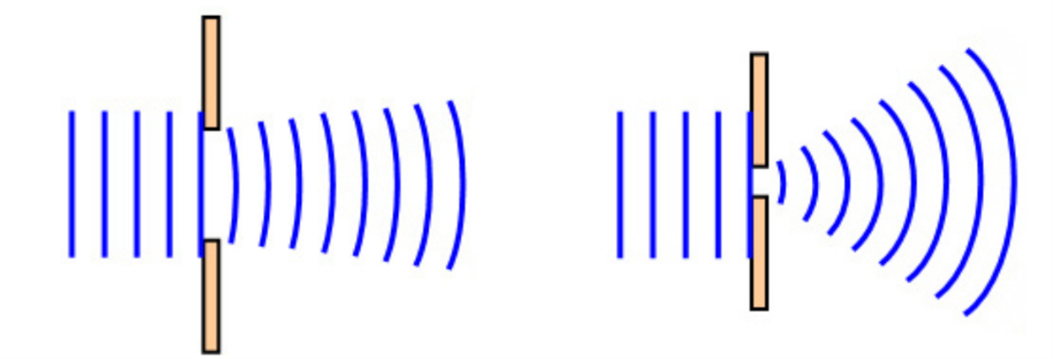
Diffraction of light through wide and narrow openings
Differences and Advantages of DOEs over Conventional Optics:
One of the significant advantages of DOEs over conventional optics is efficiency. DOEs can potentially achieve higher diffraction efficiency than conventional optics because they can redirect a large percentage of the incident light into the desired diffraction orders, whereas lenses and mirrors typically have losses due to reflection and absorption. Additionally, DOEs can be much lighter and smaller than conventional optics, especially for complex optical systems that require many lenses and mirrors. This is because diffraction gratings can be fabricated on a flat substrate, whereas lenses and mirrors require curved surfaces. DOEs also offer greater flexibility in optical design than conventional optics. With a diffraction grating, one can manipulate the amplitude as well as phase of the Light.
Non holographic DOE:
A non-holographic DOE is one that cannot be made directly in the lab with lenses and other optical tools. Instead, this kind of microstructure is a predetermined diffractive structure that changes the phase of light that passes through it. The non-holographic DOE is made digitally using coding-based software like MATLAB or Python. It has several surface features that are not sinusoidal. So, non-holographic DOE can be described with math equations, and some lithography techniques can be used to machine them directly. This article focuses on non-holographic DOE.
DOEs can be of different versions, such as amplitude-only and phase-only, as well as hybrid types containing both amplitude and phase components in the same DOE. Phase DOEs possess higher efficiency than their amplitude counterparts. Hence, for most applications, phase-only DOEs are preferred.
DOEs can be broadly categorised as:
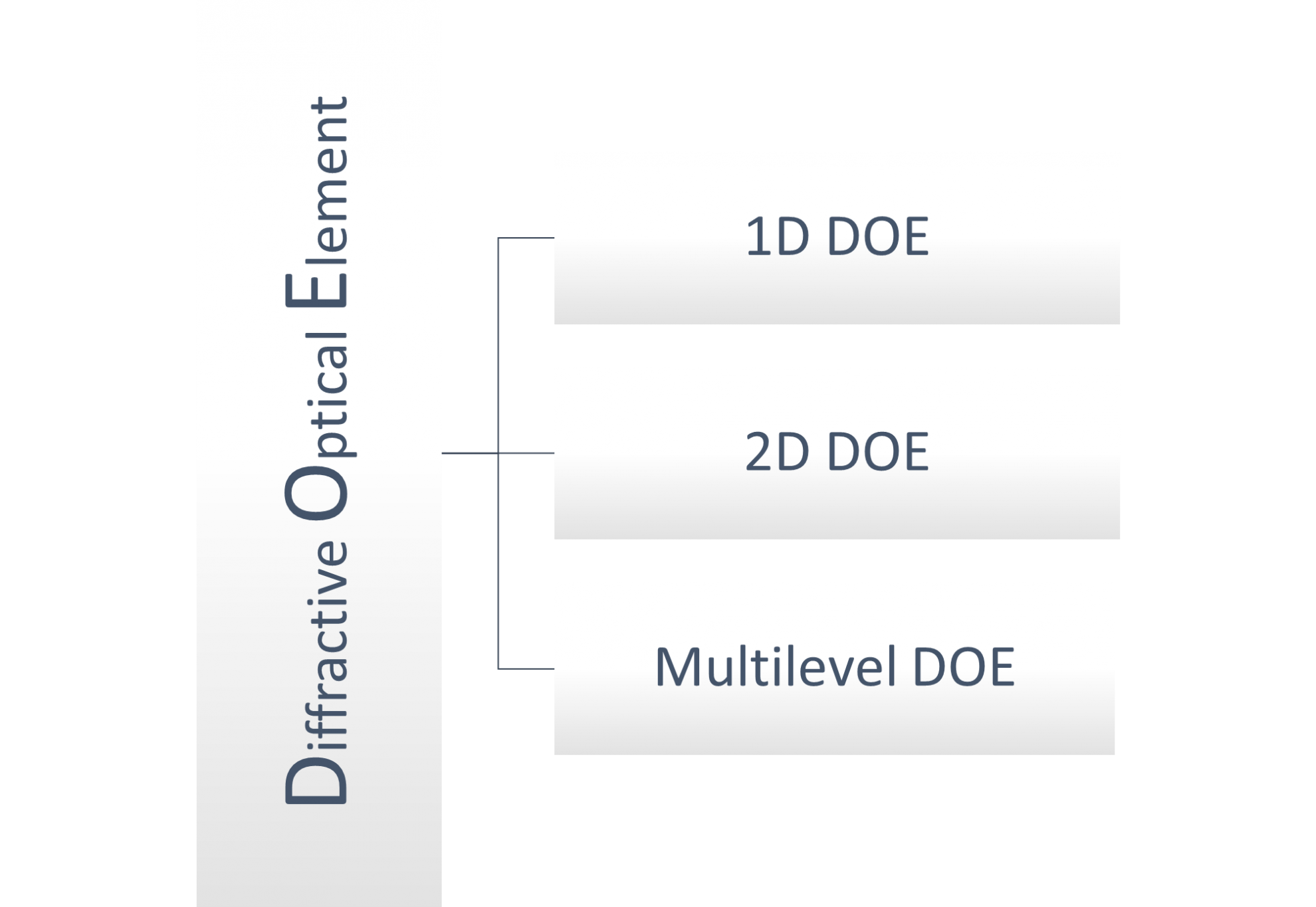
A 1D Phase DOE has phase periodicity variations in only one direction, similarly 2D phase DOE have phase periodicity variation in two direction and Multilevel phase DOEs are designed to generate a shape as close as possible to that of an equivalent Refractive or Reflective optical element to achieve high efficiency. Efficiency of Multilevel DOE > 2D DOE > 1D DOE
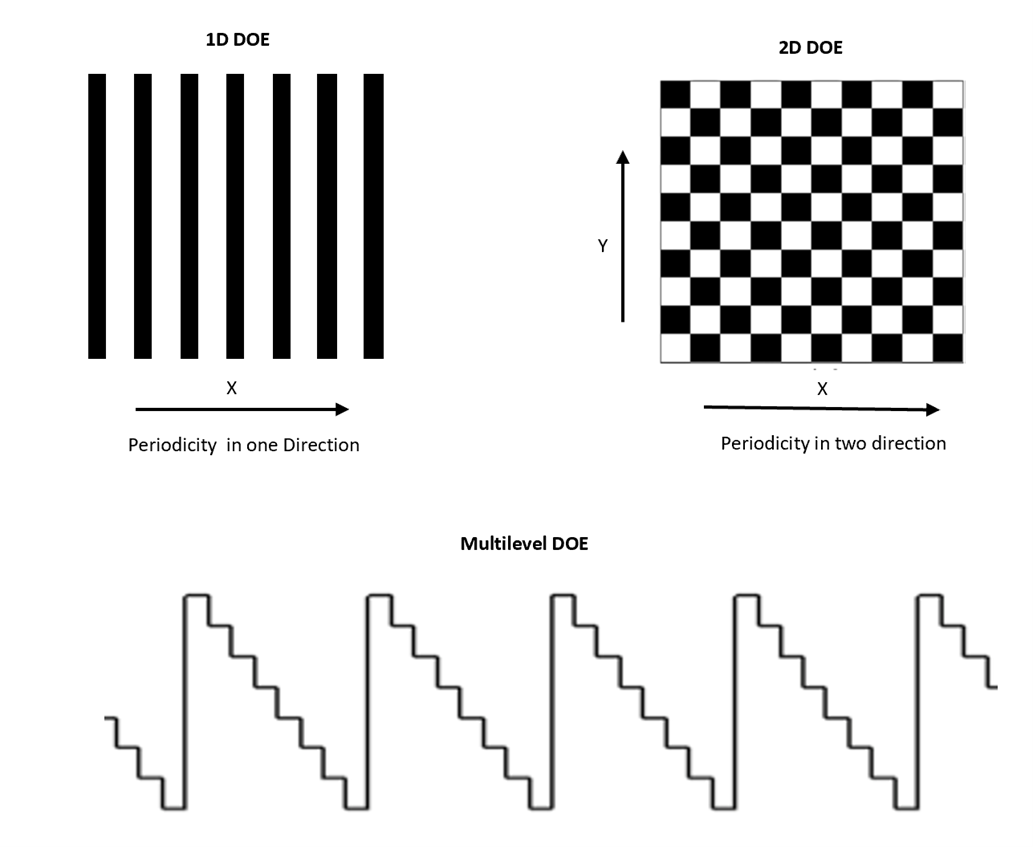
Multilevel DOEs utilize multiple levels of microstructures to manipulate light in a more intricate and sophisticated manner than their 1D or 2D counterparts. These DOEs provide greater flexibility in design due to the use of multiple levels of microstructures. Additionally, they exhibit superior efficiency compared to 1D or 2D DOEs, with the potential to achieve over 80% efficiency when designed mathematically. Multilevel DOEs also offer a high spectral range due to the use of microstructures with different periods, enabling the creation of DOEs that function over a wider range of wavelengths. Hence, multilevel DOEs are the preferred choice when designing DOEs.
Designing of DOE:
In general, there are four basic steps to design Diffractive Grating. In the first step, the constant terms are defined; these include matrix size (size of the grating) in pixels x pixels, period of the grating, wavelength, fill factor, etc. The design of the DOE is carried out in the second step, this is done by assigning complex amplitude (AeiØ) to each pixel of the matrix, where A is the amplitude transmittance, and Ø is the phase value. In the case of amplitude-only and phase-only DOEs, Ø = 0 or a constant, and A = 1, respectively. The third step is the analysis step, in which the diffraction pattern of the DOE is calculated using scalar diffraction formulae. The final step is the display step, in which the DOE amplitude or phase profile and its diffraction patterns are displayed to verify the accuracy of the code.
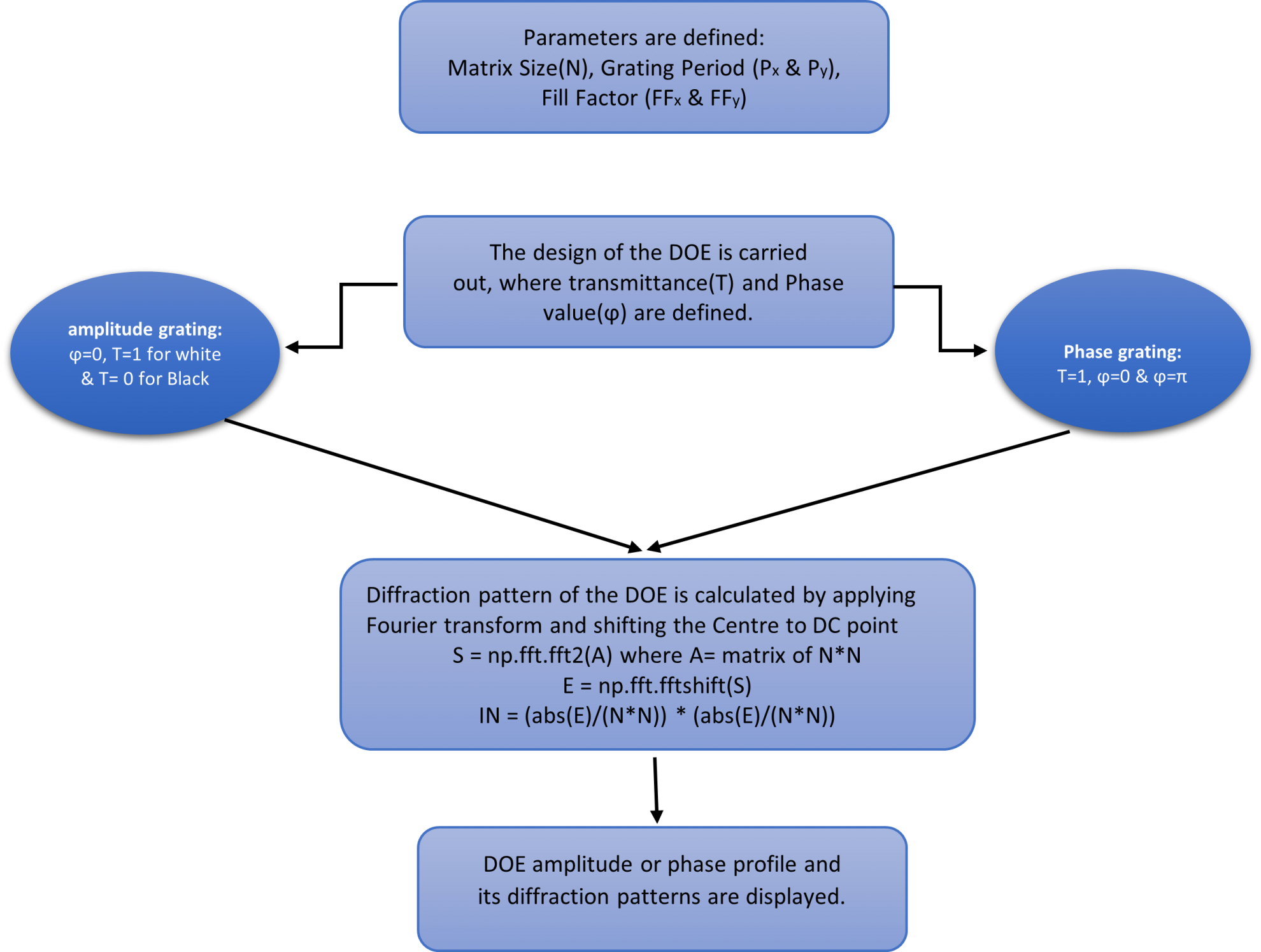
However, these methods cannot be applied to the design of DOEs that generate any arbitrary intensity profile at the Fourier Plane (Plane where we will get the Fourier transform of the incoming beam) and moreover these methods lack the potential to get back the phase value from the Diffraction pattern i.e., the process does not work in the reverse direction. To design DOE that generate arbitrary Intensity Profile at the Fourier plane (IFTA) can be used. The IFTA can also be used in the design of automobile signaling lighting, such as turn signals, brake lights, etc. These lights require specific spatial distributions to be easily recognizable by other drivers. By calculating the Fourier transform of the desired signal distribution, the IFT algorithm can be used to determine the microstructure required to achieve the desired signal pattern. The IFT algorithm can be a useful tool in designing automobile signaling lighting that is easily recognizable and provides clear communication to other drivers on the road
Design procedure of arbitrary pattern using the IFTA (Gerchberg–Saxton algorithm):
The IFTA works by using known input information (Image) at the source plane to calculate the (grayscale) phase of a DOE that will generate the desired intensity pattern at the target plane. At the source plane, a random phase profile is generated between 0 to 2π. The corresponding phase values are extracted after Fourier transformation of this phase-amplitude profile. The extracted phase values are assigned to the appropriate pixel locations in the target intensity profile, and the inverse Fourier transform is computed. The phase profile that results replace the phase profile at the source plane. This is the first cycle or iteration. The phase profile calculation’s accuracy increases with the number of iterations until it reaches a constant value. The number of iterations can be reduced by selecting an appropriate initial phase profile or setting the error value to the required number where after reaching the value the process stops. Using IFTA Method (Gerchberg–Saxton algorithm) any desired DOE matrix can be simulated to calculate its Phase value an important parameter in image processing moreover IFTA can also be used for digital hologram generation from a digital image using phase-only information.
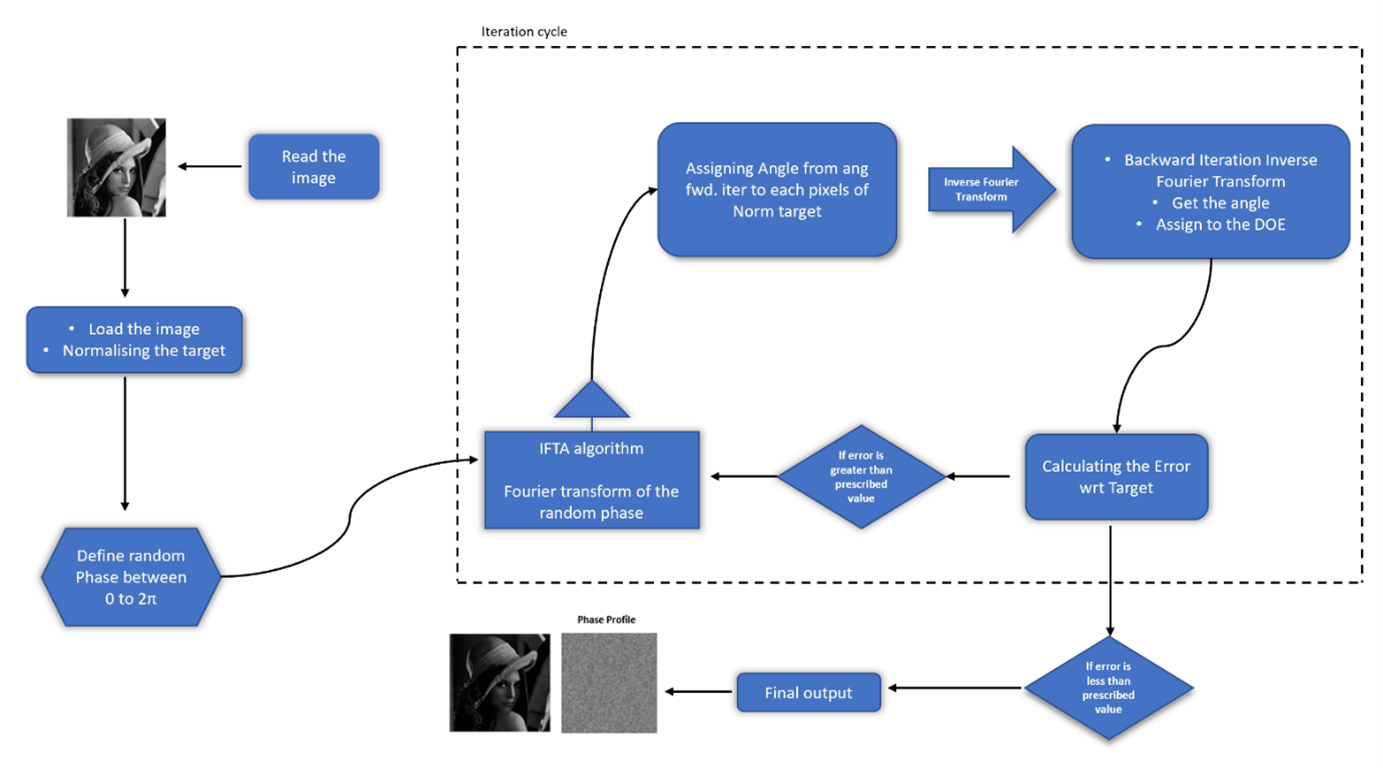
Although the IFTA is very powerful (they can be used to create DOEs that generate almost any intensity pattern), their main problem is that there is no specific phase relationship from one pixel to another. This leads to scattering and, hence, an overall decrease in efficiency and contrast of the final image and convergence is slow and only an approximate solution can be obtained.
Application of DOE:
Summary:
In this article, we describe a novel and adaptable strategy for an automotive lighting system based on diffractive optics. The method is based on diffractive optical elements (DOEs) that diffract the incoming light in multiple diffraction orders to generate a specified pattern that satisfies the required specifications. Diffractive optics are a powerful solution for improving the efficiency and functionality of automobile lamps. By manipulating light using micro-structured patterns, diffractive optical elements (DOEs) can create more precise lighting patterns for Automotive lamps. This results in better visibility, reduced glare, and improved energy efficiency. DOEs are lightweight and require less material, making them a cost-effective solution. Overall, diffractive optics are a versatile and powerful technology that can improve the safety and performance of automobile lighting systems. Hence, what has been presented is a process that allows user to work with DOE theoretically that can smaller, lighter, and less expensive with greater flexibility
Reference:
